최장 증가 수열이라고 불리는 Longest Increasing Subsequence (LIS)라는 문제는 간단하지만 강력한 문제 중 하나이다. 이 문제는 다이나믹 프로그래밍을 활용한 $O(N^2)$ 풀이와 이분 탐색을 활용한 $O(NlogN)$ 풀이가 잘 알려져 있는데, 이분 탐색을 활용한 풀이가 어떻게 최적화되었는지에 대한 설명을 이 글에서 적고자 한다.

Naive solution: Bruteforcing

간단하게 생각해보자. 모든 부분 수열에서 오름차순을 이루는지 확인해보면 된다. 모든 원소가 부분 수열에 속하거나 속하지 않는 두 가지 상태를 가진다. 길이 $N$의 수열이라면 $2^N-1$개의 부분 수열이 있고, 각각 오름차순으로 확인해야 하므로 $O(N\times 2^N)$이라는 악마같은 시간복잡도가 튀어나온다. 이 시간복잡도로는 $N$이 $30$ 정도만 넘어가도 시간 내에 해결하기 어렵다.

Better solution: Dynamic Programming

몇 가지 생각을 통해 문제를 빠르게 해결할 수 있다. 이전 증가 부분 수열의 가장 끝 값보다 큰 값이 뒤에 나온다면, 이전 수열 뒤에 큰 값을 붙이는 것만으로 증가 수열의 길이를 늘릴 수 있다는 아이디어에서 나온다.

‘$i$번째 수로 끝나는 증가 수열의 길이’ 배열을 통해 DP로 문제를 해결할 수 있다.

아래 그림을 보자. 아래 그림의 $x$축은 배열의 인덱스를 의미하며, 점의 높낮이는 배열의 값을 의미한다. 점에 쓰인 수는 해당 인덱스로 끝나는 증가 수열의 길이이다. 앞으로도 해당 그래프를 사용해서 설명할 것이므로 익혀두자. 아래 점들은 배열을 그래프로 나타낸 하나의 예시이다. 배열의 정확한 값은 중요하지 않고, 상대적인 관계가 중요함에 유의하자.

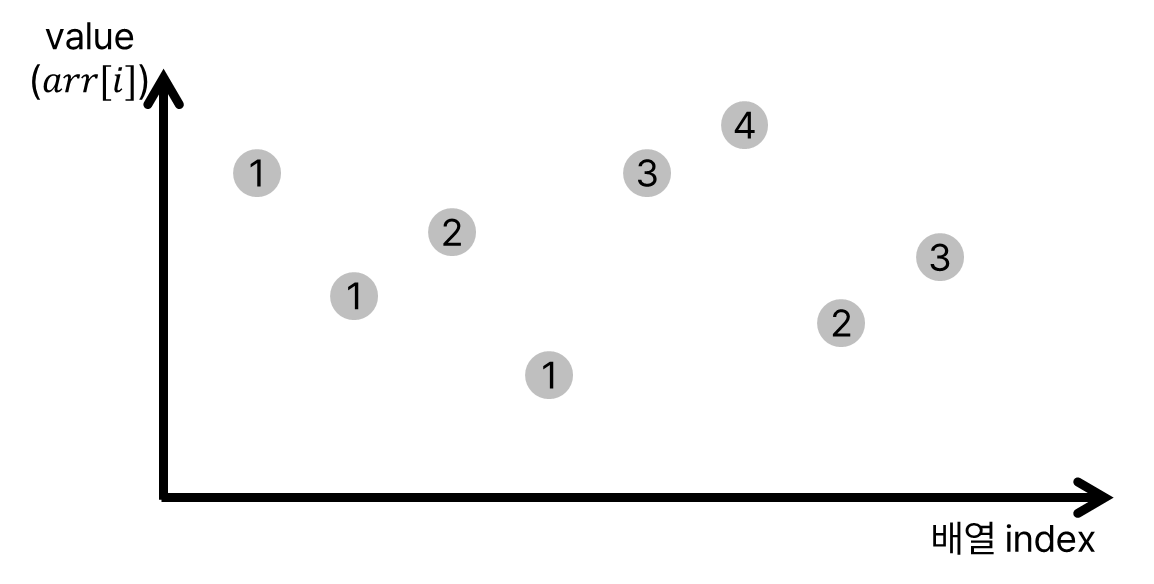
해당 그래프에서는, 자신보다 왼쪽에 있는 점(앞쪽 인덱스)에 대해서 아래에 있는 점(더 작은 값)에 적힌 수의 최댓값에 $1$을 더한 것과 같다. 앞쪽 증가 수열에 자신을 붙임으로써 길이를 늘릴 수 있기 때문이다. 이 경우, 앞의 증가 수열에 대한 모든 정보를 저장해야 한다. DP식을 세우면, 아래와 같은 점화식을 통해 문제를 해결할 수 있다.

$$d_i = \max_{j<i}(d_j) + 1$$

앞에서도 말했듯, 해당 DP 풀이법은 앞의 증가 수열의 길이를 모두 기억해야하는 단점이 존재한다. 따라서 모든 경우를 따져보는 풀이법보다는 훨씬 빠르게 동작하지만, 여전히 조금 느리다. $O(N^2)$ 풀이로, $N = 1\ 000$ 정도는 빠르게 해결할 수 있지만 더 긴 수열에 대해서는 점점 느려지는 성능을 보인다.

Faster solution: Binary Search

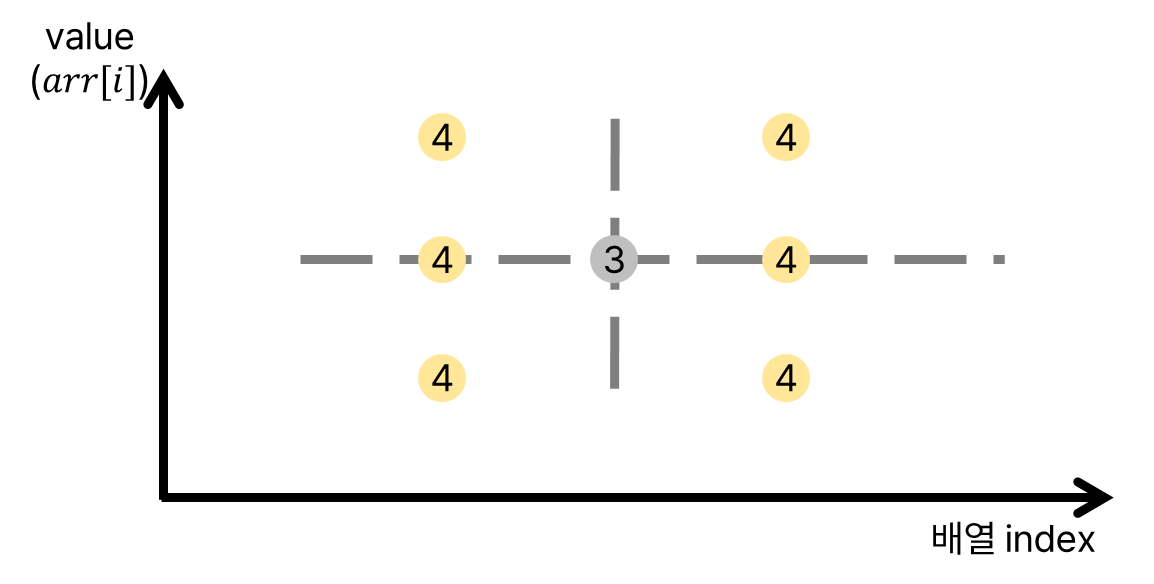
이 문제를 더 빠르게 해결하는 방법으로 이분 탐색을 활용한다. 이를 이해하기 위해서는 몇 가지 성질을 관찰해야 한다. 아래와 같은 배열(그래프)을 보자. 회색 점이 이미 찍혀있는 점이고, 그 중 증가 수열의 길이가 $3$인 점이 아래와 같이 존재한다.

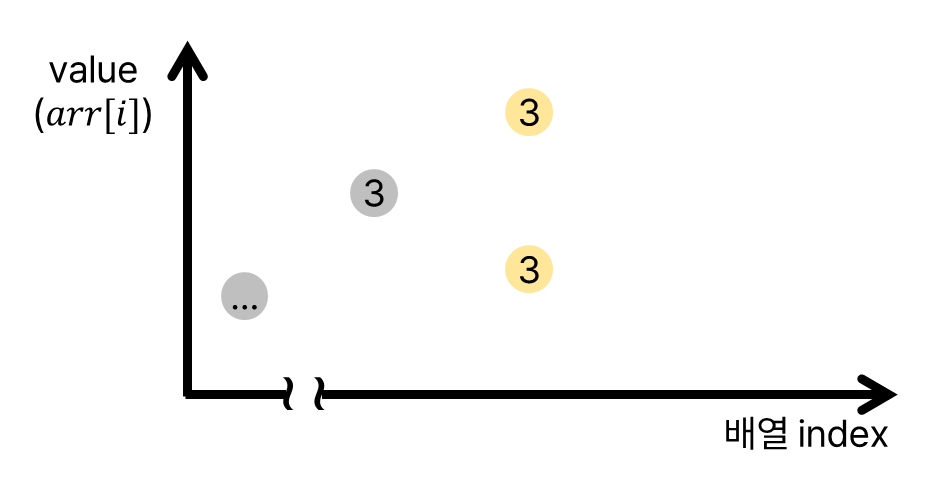
배열의 다음 수(노란색 점)가 들어올 때, 해당 수가 길이 3의 부분수열을 가지려면 어디에 존재해야 할까?

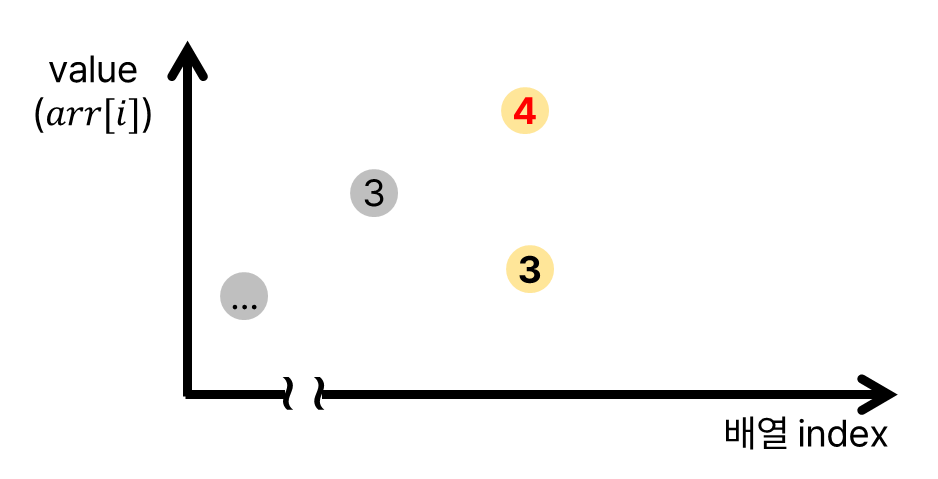
더 큰 수는 길이 $3$으로 들어올 수 없다. 기존의 회색 점을 받아서 길이 $4$의 증가 부분 수열을 만들 수 있기 때문이다. 따라서 같은 길이를 가지는 증가 부분 수열의 길이가 뒤쪽에 다시 등장한다면, 해당 값은 같거나 더 작다.

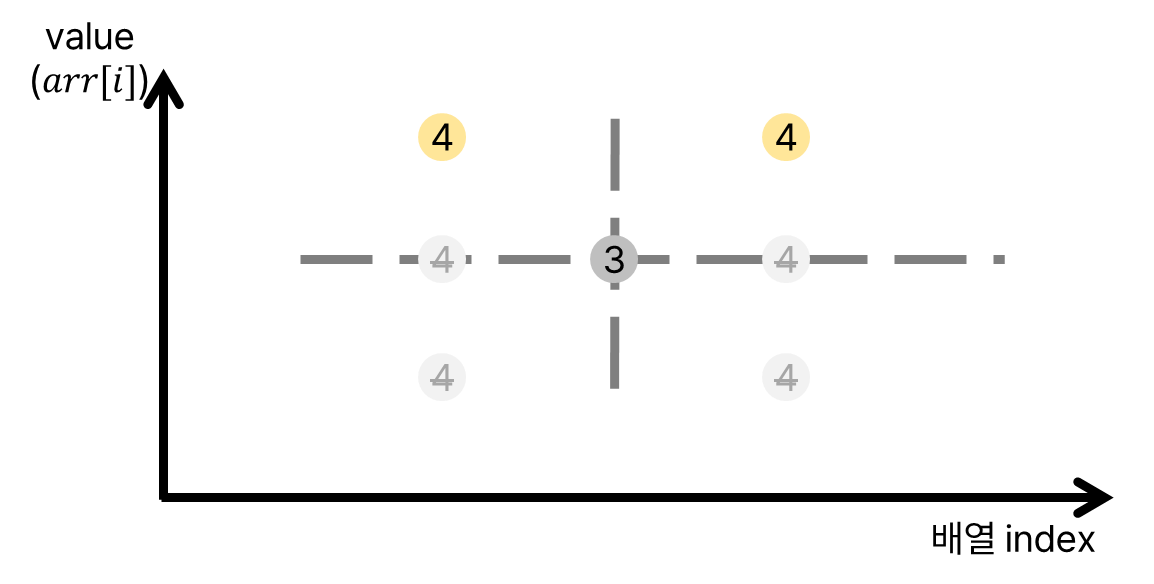
배열에서는 같은 길이를 가지는 부분 증가 수열에 대해서, 더 작은 값을 기억해둬야 한다. 그래야 부분 증가 수열의 길이를 더 길게 늘려 최종적으로 LIS를 구할 수 있기 때문이다. 아래 그림에서 처음 두 값에 대해서 증가 부분 수열의 길이는 모두 $1$이지만, 세 번째 수가 등장할 때 실제로 증가 부분 수열의 길이를 늘리게끔 하는 값은 더 작은 값임을 알 수 있다.

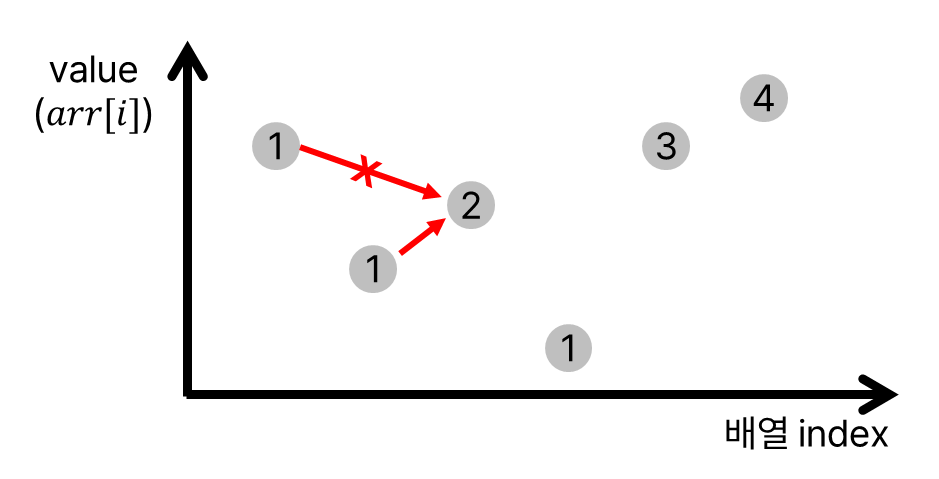
같은 증가 부분 수열의 길이에 대해서는 더 작은 값을 기억해야 하지만, 더 작은 값은 나중에 등장하므로 가장 나중에 등장하는 값을 기억하면 된다.

두 번째 관찰을 해 보자. 마지막으로 기록한 길이 $3$의 증가 부분 수열을 가지는 값이 아래 회색 점이라고 하자. 다음 여섯 개 점 중에서, 길이 $4$의 증가 부분 수열을 갖는 값이 올 수 있는 점은 어떤 점일까?

회색 점보다 큰 값을 가지는 두 가지 경우는 모두 가능하다.

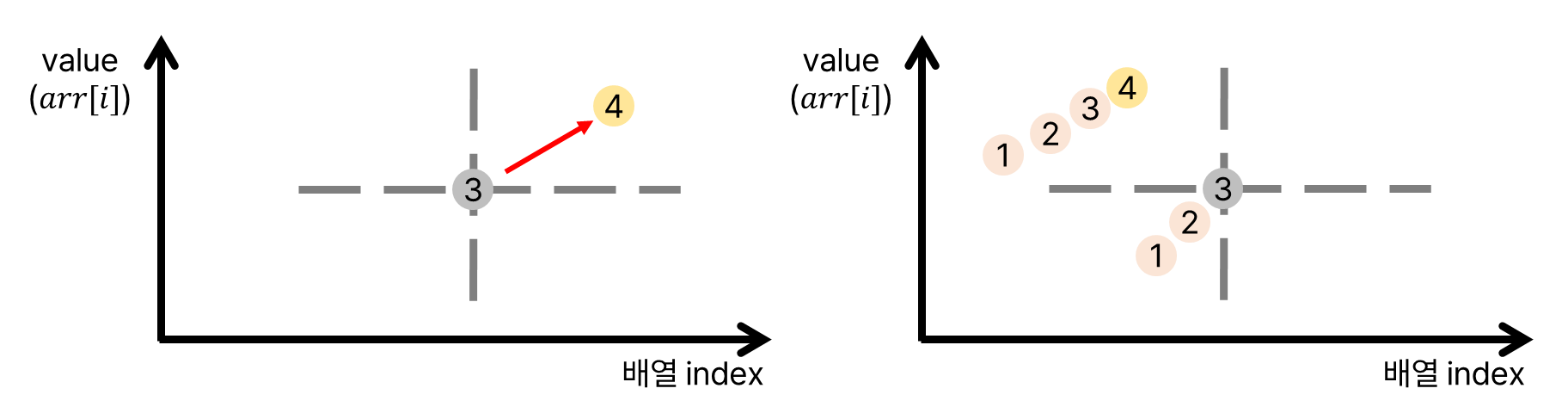
같은 경우에는 불가능하다. 앞쪽에 길이 $4$의 증가 부분 수열이 존재하는 경우, 해당 증가 부분 수열의 앞쪽 세 개를 받아서 길이 $4$가 될 수 있다. 뒤쪽에 존재하는 경우에는, 해당 회색 점이 마지막으로 기록한 길이 $3$의 증가 부분 수열 값이 아니다. 더 낮은 값이 존재해 뒤의 노란 점을 길이 $4$로 만드는 다른 길이 $3$의 점이 존재한다.

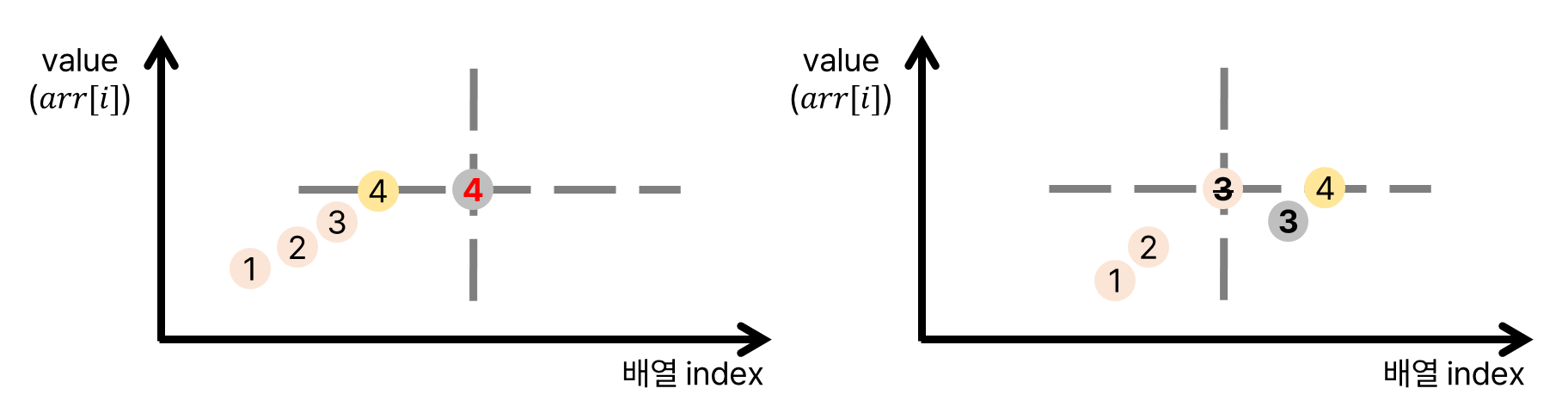
같은 논리로, 더 작은 값의 경우에도 불가능함을 보일 수 있다. 앞쪽에 길이 $4$의 증가 부분 수열이 존재한다면, 해당 값을 받아 길이 $5$의 증가 부분 수열이 될 것이다. 뒤쪽에 존재한다면, 회색 점이 마지막으로 기록한 길이 $3$의 증가 부분 수열 값이 아니다.

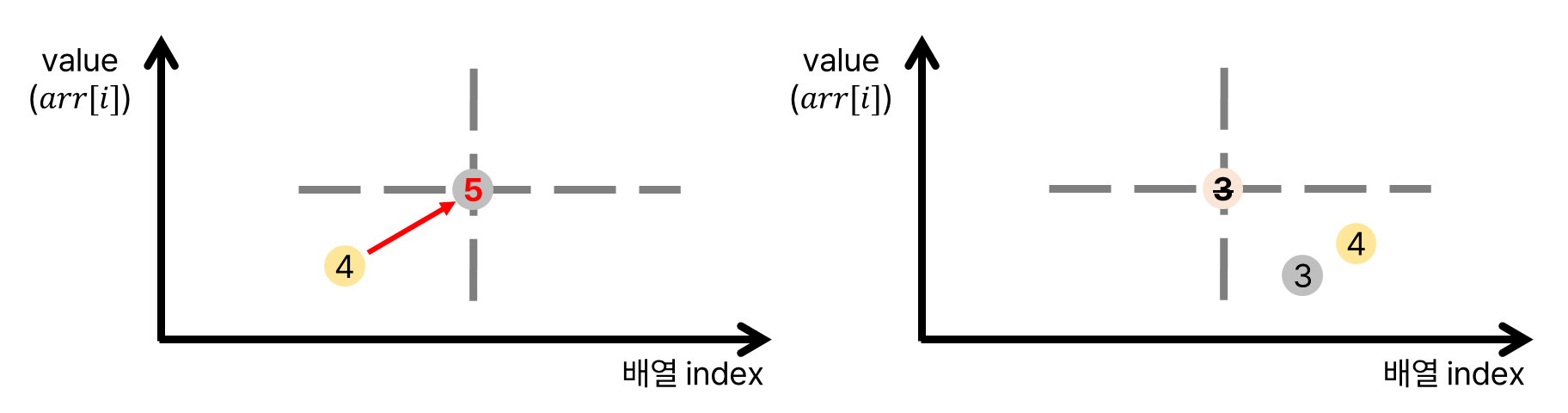
따라서 길이 $3$의 증가 부분 수열의 어떤 점에 대해서, 길이 $4$의 증가 부분 수열을 이루는 점보다 더 작은 곳에 존재한다. 일반화하면, 길이 $i$의 증가 부분 수열을 가지는 어떤 점에 대해서, 길이 $i+1$의 증가 부분 수열을 가지는 점들은 더 큰 값을 가진다.

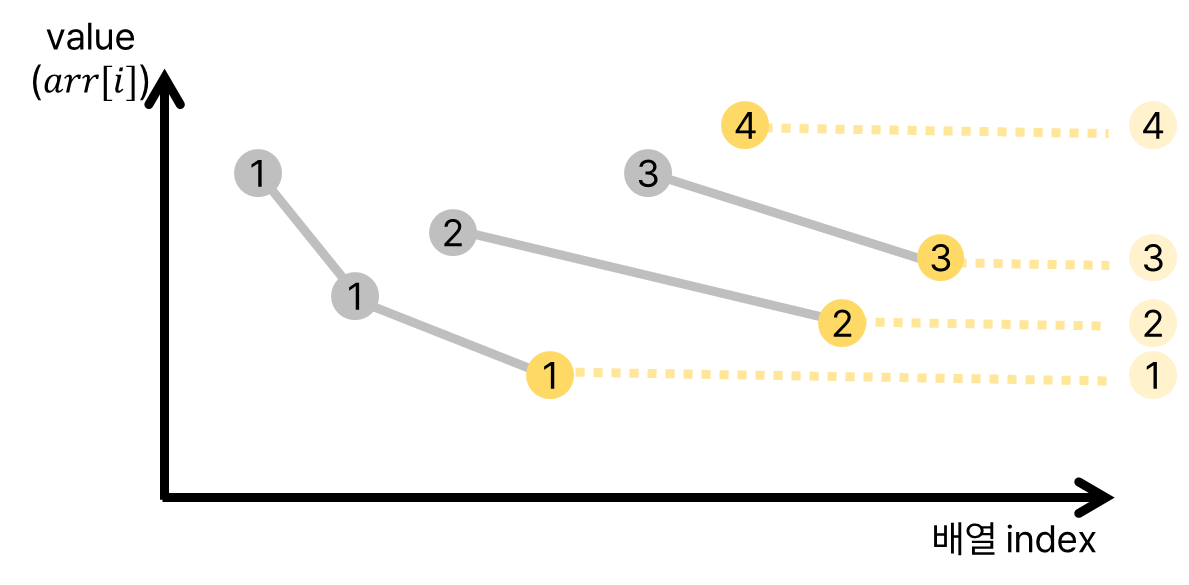
관찰을 통해 두 가지 사실을 알아냈다. 첫 번째는 같은 길이의 증가 부분 수열에 대해서는 나중에 나오는 값이 더 작다는 것이고, 두 번째는 길이 $i$의 증가 부분 수열을 가지는 어떤 점에 대해서, 길이 $i+1$의 증가 부분 수열을 가지는 점들은 더 큰 값을 가진다는 것이다. 두 가지 사실을 가지고 새로운 결과를 하나 도출해낼 수 있다.

길이가 같은 증가 부분 수열을 이루는 점들을 서로 잇는다면 선분들은 서로 교차하지 않을 것이고, 더 긴 증가 부분 수열을 이루는 점이 더 위에 존재하게 된다. 이때, 같은 길이 중에서도 나중 값(더 작은 값)을 기억해야 하므로, 해당 점을 진한 노란색으로 표현했다. 마지막으로 기억하는 값은 각 증가 부분 수열의 길이에 대해서 오름차순임을 볼 수 있다. 값이 오름차순으로 표현되므로, 우리는 이분 탐색을 사용할 수 있다.

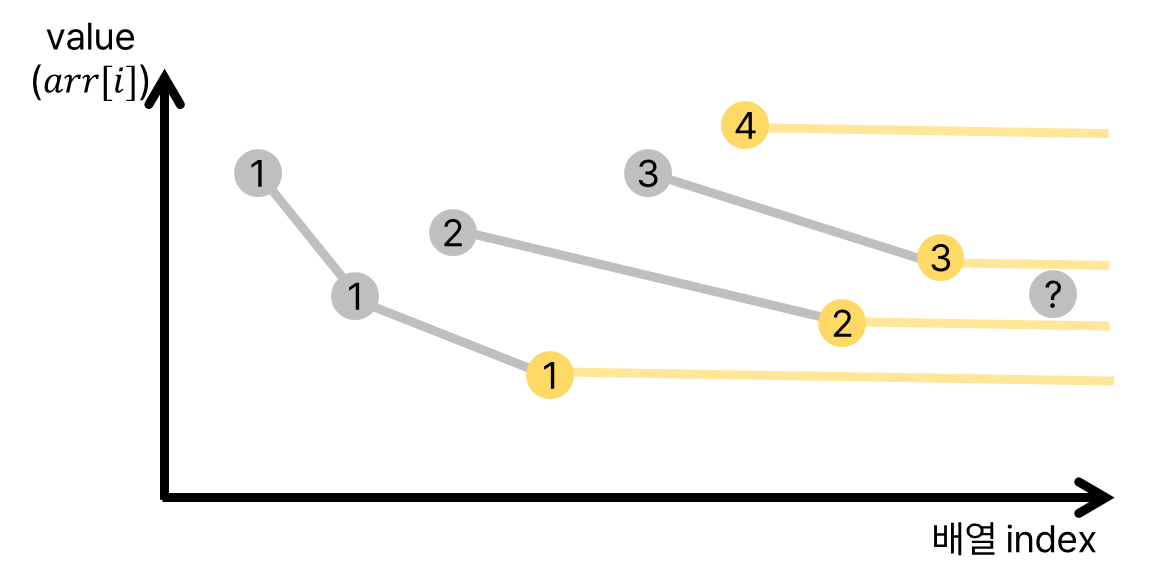
만약 새로운 값이 등장한다면, 증가 부분 수열의 길이는 어떤 부분 수열의 길이를 나타내는 값 사이에 존재하게 된다. 새로 들어온 값이 마지막 값이 되도록 하는 (가장 작은 값이 되도록 하는) 증가 부분 수열의 길이를 구해야 한다. 이는 이분 탐색을 통해 빠르게 구할 수 있다. 각 증가 부분 수열의 가장 작은 값을 기억해두고 있기 때문이다.

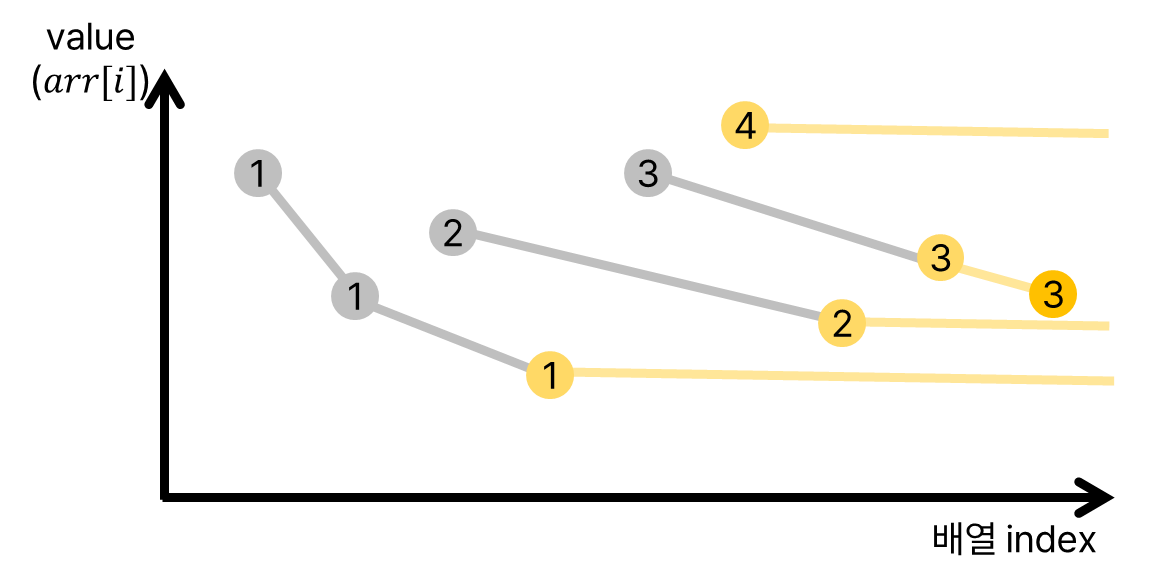
따라서 길이 $i$의 증가 부분 수열중 가장 작은 값을 저장하는 배열을 만들어둔 뒤, 새로 들어오는 값들에 대해서 각각 계산을 통해 증가 부분 수열의 길이를 적절하게 구해주면 된다. 이 경우의 시간복잡도는 $O(NlogN)$이다. 이제 $N$이 $200\ 000$ 이상의 큰 수가 들어오더라도 빠르게 문제를 해결할 수 있게 되었다!

많은 알고리즘들을 동작하도록 쓰는 것은 쉽다. 하지만 원리를 모른 채 블랙박스 형태로 문제를 해결하다 보면 근본적인 원리를 활용해 해결하는 문제를 풀기 어려워지는 순간이 온다. LIS 문제들도 원리를 모르는 채로 사용하던 때가 많았기에, 이 기회를 통해 제대로 이해할 수 있어 좋았다 😋 특히나 솔브드 기준 플래티넘 이상의 문제 중에서 태그를 까 봤더니 LIS 문제였던 경우도 적지 않았기에, 해당 문제들을 자력으로 풀 수 있으려면 이런 원리는 꼭 잘 알아둬야겠다. 👏